There are many sorting algorithms out there that are widely accepted: Insertion sort, quick sort, heap sort, merge sort, bucket sort… and so on and so forth. There are a lot of qualities of each sorting algorithm that allow you to choose what algorithm fits your requirements, but one of the sorting algorithm qualities I want to talk about in this post is stability.
Sorting stability
Stability of a sorting algorithmn is the label that indicates whether or not it will preserve the order of two or more elements in the array if they have equal sorting keys. A sorting algorithm is stable if it preserves the order of multiple elements with the same keys. Conversely, a sorting algorithm is unstable if it cannot guarantee order preservation of multiple elements with equal keys.
An example in real life: There is a line of people that need to be ordered by age. If there are two people with the same age standing in line, the sorter would be using a stable approach if there is a guarantee that their order in line relative to each remains the same.
When does stability matter?
Sorting stability is interesting by itself, but when do we care about it? We care in a situation when we require the output to have the guarantee of preserving order for duplicate keys.
Example data
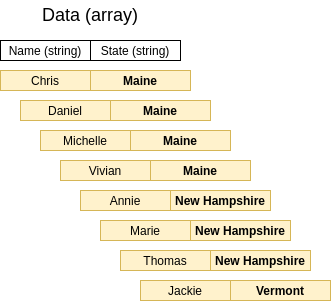
Let’s see another example and dissect it. Let’s say we have an array of data, where each element has two fields: Name and State. Here is a visual respresentation of the data:
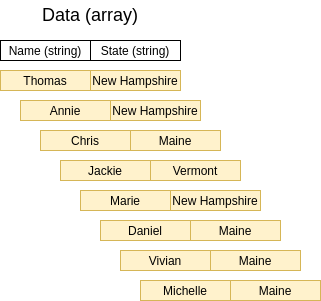
Requirement
Sort the data by state and then by name, so that the final data is ordered by state first and then by name.
Approach
This data will be sorted twice so that the requirements can be met:
- Sort first by
Name - Sort second by
State
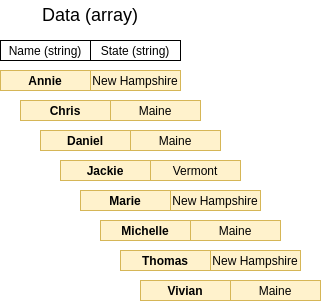
The first sort by Name doesn’t require a stable sorting algorithm, as the order for duplicate sorting keys (names) doesn’t matter. So in this case, we could do a heap sort (a naturally unstable sorting algorithmn) on this array by name.
The output from sorting by Name is:
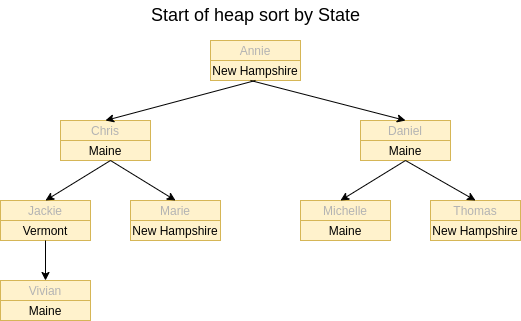
The second sort by State is where it can get interesting. If we were to try a heap sort by State, this is how we would setup our complete binary tree:
If we were to continue the heap sort by State, we would end up with an array sorted like:
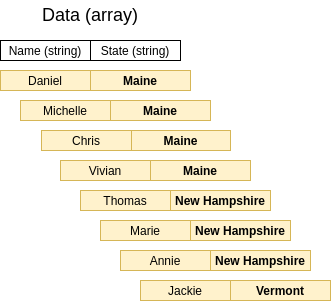
Yes, the array is sorted correctly by State, but let’s see how the elements themselves transitioned:
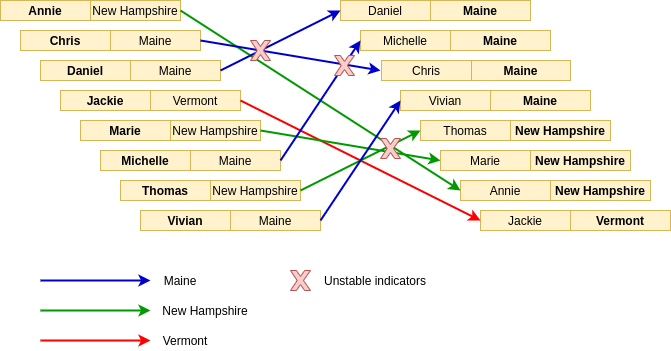
The fact that elements with the same sorting key (State) have overlapping sections to the destination array elements indicates that their order was not preserved, showing that this is a unstable sorting algorithmn.
The solution
If we were to look back at the requirements, the heap sort by State does not work: The output is sorted by State but it is no longer sorted also by Name within each State.
Let’s try doing a second sort (by State) with a naturally stable sorting algorithm: Merge sort. The output of the second sort if we were to use a merge sort (instead of a heap sort) would be:
Of course, State is correctly sorted but now let’s see how the elments transitioned from being sorted by Name to a merge sort by State:
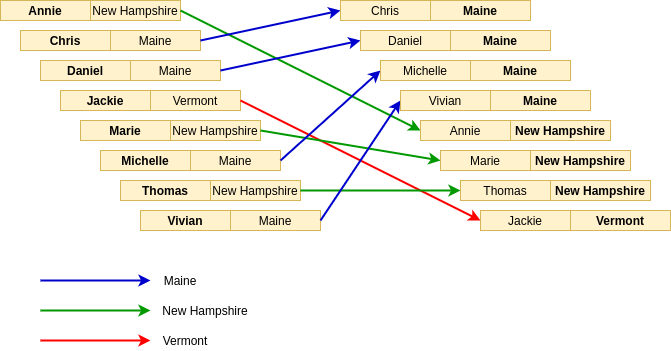
Now because we used a stable sorting algorithmn (merge sort) on State, we preserved the order of elements with the same State key value, giving us the desired output of a dataset that is sorted by state and then by name.
Summary
Sorting algorithmns are a large part of computing, and understanding the behaviors of different algorithms will help in determining the right one for your requirements.
